Introduction

Last winter, I worked on a personal project I call ongaku (from the Japanese for ‘music’). This was an attempt to use manifold learning to create a metric space for music. The preprocessing relied heavily on a method called (Valero and Alias 2012). This method was intended to replace Mel Frequency Cepstral Coefficients. Where Mel Frequency is a logarithmic transformation of sound frequency, in an attempt to simulate human perception of sound. The most common transformation for Mels is:

\[ m = 2595 \log_{10}{1 + \frac{f}{700}} \]

This simple approach works very well, but it has its basis in human perception which is a tricky thing. There’s no reason to believe that the brain makes judgments based on human perception. It’s very possible that the brain takes in data, and produces two perceptions, one of the sound itself, and the other as the semiotic interpretation of that sound. Enter the Gammatone Cepstral Coefficients. This is a simplification of the process that sound signals undergo when being transferred through the cochlear nerve, the nerve that transfers data between the ear and the brain. So the theory goes, this will allow a machine learning algorithm to work with data that better simulates how the brain receives sound signals, rather than how the mind perceives them. Research has shown that GFCCs outperform MFCCs in machine learning tasks (Liu 2018). The gammatone transformation looks like:

\[ g_q(t) = t^4 e^{-54 \pi t + j 20 \pi t}u(t) \]

I have been able to find an implementation of the gammatone transformation in python, but it’s slow, and is a port of a MATLAB plugin. This package is intended to mimic that package’s structure, but instead working natively in OpenCL for speed. This is problematic for a number of reasons. First, the MATLAB plugin has been shown to be inefficiently implemented (Ma, n.d.a) (Ma, n.d.b). Secondly, for my purposes, gammatones need to be processed on long files, 2-10 minutes in length, and even Dr. Ma’s implementation runs serially. As such, I believe that an inherently parallel version of this would be a benefit, not only to me, but to the scientific computing community at large. As such, this project will be released on pypi as gammatone. There does exist a github project called gammatone which is the implementation that ongaku currently uses, but it is not avaliable on pypi at the time of writing, so there will be no conflicts in the long run.

Implementation

The available implementations of gammatone filters are serial. However, there have been a number of attempts to parallelize IIR (Infinite Impulse Response) filters in the past(Anwar and Sung, n.d.) (Belloch et al. 2014). The general consensus is that this is rarely better than a serial implementation, and the implementation of a new filter needs to be made bespoke for that filter. After analyzing the implementation methods, I decided that (for now,) this is beyond the scope of this project. The fourth order gammatone filter is implemented like:

\[ erb(x) = 24.7 * (4.37 \times 10^{-3} + 1) \] \[ \delta = e^{\frac{2 \pi}{f} erb(f_c) \times 1.019} \] \[ q_t = \cos{\frac{2 \pi}{f} f_c} + i\sin{\frac{2 \pi}{f} f_c} \] \[ g = \frac{\left(\frac{2 \pi}{cf} erb(f_c) \times 1.019\right)^4}{3} \] \[ y_{t} = q_t x_t + 4 \delta y_{t-1} - 6 \delta^2 y_{t-2} + 4 \delta^3 y_{t-3} - \delta^4 y_{t-4} \]

Where \(f\) is the sampling frequency of the signal, and \(f_c\) is the target frequency to test membrane resonance against. The basilar membrane displacement (\(B_t\)) and Hilbert envelope (\(H_i\)) are defined with simple transformations. The cochleagram uses the Hilbert envelope to construct an image.

\[ B_t = g y_t q_t \] \[ H_t = g \sqrt{y_t^2} \]

Another option is to use a prefix sum (Blelloch, n.d.). The problem with this is that while a single prefix sum can be exact to the first order of a filter, most implementations of gammatone cochleagrams use a fourth order filter. However, most implementations are made for medical applications, and I am a social scientist. Implementing a first order gammatone filter can, unlike higher order filters, can be reduced to a one-dimensional prefix sum operation (Blelloch, n.d.). A prefix sum is generally defined with an operator \(a \oplus b\) such that:

\[ y_t = \bigoplus_{\forall t} x_t \] \[ y_t = x_0 \oplus x_1 \oplus \cdots \oplus x_t \]

For a first order gammatone filter we can define:

\[ a \oplus b = \alpha \delta a + b \]

Then implementing the gammatone filter is a matter of finding the best \(\alpha\). Based on the original description of gammatone filters, we’ll set \(\alpha = -.67\). It must be negative so that the filter can resonate with the input signal (Shen, Sivakumar, and Richards 2014).

Results

In comparison with the detly implementation, testing across all of the songs in the album Traffic and Weather by Fountains of Wayne (Wayne 2007). These songs are 2 minutes, 58 seconds on average. On my laptop, which has an Intel Core i7-7700HQ CPU @ 2.8GHzx8 processor and a GeForce GTX 1080 Max-Q GPU, the detly implementation (serial) takes 7.5 seconds to create a 16-level Cochleagram (16 gammatone filtrations) for a single song on average. The GPU implementation takes 1.75 seconds for a single song on average. This is a little more than a 4x speedup.

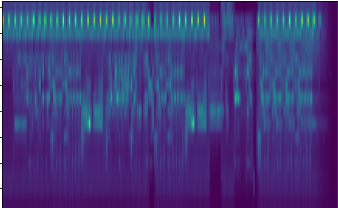
Figures 1 and 2 show the old and new implementation’s cochleagrams. Notice that the new implementation has a “squishy” quality to it. Which is expected since it’s a much less complicated implementation. Despite the lack of clear definition, a machine learning technique should still be able to identify aural features.

Future

While creating a higher order implementation of the gammatone filter and therefore the cochleagram is outside the scope of this project, I believe it can be done given more time and outside research. A possible pathway is to create a “horizontal” kernel, that runs multiple fourth order gammatone filters at once. Another approach is to convert the signal to frequency space, and then apply multiple frequency space filters to the signal in a cascading manner (Holdsworth, Patterson, and Nimmo-Smith, n.d.). Even though this project has resulted in a small step in the right direction, it could ultimately unlock the door for more accessible social science research on audio content.

References